Why in nature does a group of individuals move or act in a coordinated manner even in the absence of explicit guidance or rule directing this coordination? This phenomenon is the result of a series of reciprocal interactions that cause people to act in synchrony.
A group of researchers, Timoteo Carletti (University of Namur), Lorenzo Giambagli (University of Florence and Namur) and Ginestra Bianconi (Queen Mary University of London)
studied this phenomenon, publishing the research in Physical Review Letters and helping to shed light on this type of phenomenon in poorly understood scenarios. Indeed, when interacting are currents or flows or dynamical variables associated with groups of more than two interacting elements, the situation is considerably more complex, and synchrony may be more delicate to achieve.
"A paradigmatic example of synchronization is when, at a concert or presentation, audience members are found clapping in unison, simultaneously." - Explains Lorenzo Giambagli, a Joint PhD student in between Italy and Belgium - "But there are many other examples, such as when certain chemicals react with each other, or when electrical signals in our brains move together."
To understand how synchronization works, we can think of everything that interacts as a point, or "node." When two nodes interact, we can connect them with a line, or "link." Together, the nodes and links form a network. However not only individual things interact with each other. Sometimes, groups of two, three or more nodes work together.
Consider, for example, signals on the synapses of neurons. In this case, it becomes necessary to talk about a signal concerning the interaction between two elements (the two neurons in connection).
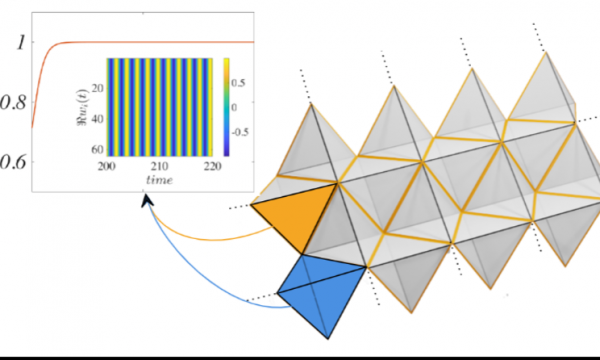
This kind of concept can also be extended to consider signals involving an interaction between three elements, represented by adding filled triangles to the network, and so on.
Doing so results, depending on the system being described, in complex geometric structures such as the one shown, called Simplicial Complexes or Cell Complexes.
"By means of mathematical tools from Algebraic Topology it was possible to predict the attainment, or not, of synchronous states involving all these different classes of signals. " - Lorenzo Giambagli concludes - "With this study, we have revealed the crucial role of the global features of the structure of interactions that characterizes the system (the simplicial complex). Indeed, it is the topological features such as holes or cavities that allow the global synchronization of the signals to be achieved or not."
Full article: